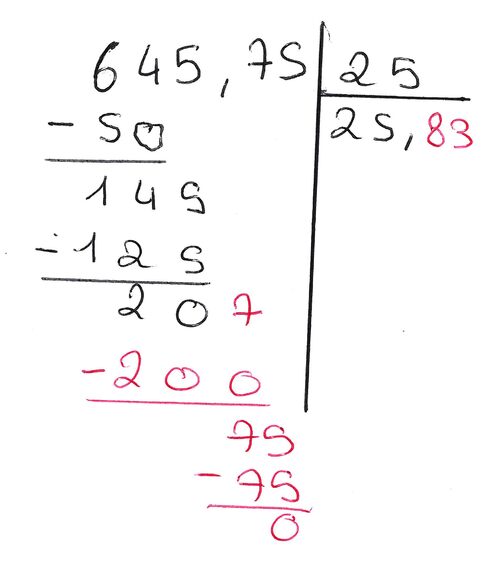Les nombres décimaux (2) Décomposition et comparaison

Rappel :

1) Décomposer les nombres décimaux

0,346 = ( 0 + ) 3/10 + 4/100 + 6/1000 = ( 3 x o,1 ) + ( 4 x 0,01 ) + ( 6 x 0,001 ) 

143,09 = 100 + 40 + 3 + 9/100 =

( 1 x 100 ) + ( 4 x 10 ) + ( 3 x 1 ) +

( 9 x 0,01 ) 

3,25 = 3 + 2/10 + 5/100 =

( 3 x 1 0) + ( 2 x 0,01 ) + ( 5 x 0,001 )

2) Comparer les nombres décimaux 

Pour comparer deux nombres décimaux on compare d'abord les parties entières .

Exemples : 5,37<6,09     car

5<6

Je compare en commençant par la gauche, ici les unités .

Si les parties entières sont égales, on observe la partie décimale en commençant par les dixièmes, les centièmes, les millièmes .

Exemples : 7,5 <7,8

car 5 dixièmes <8 dixièmes

4,19 >4,12

car 9 centièmes >2 centièmes

25,351 <25,352

car 1 millième <2 millièmes

                                             La division (3)          

Je veux calculer 15/2

Je pose la division:

      Le reste 1 doit être diviser par 2, pour cela il faut procéder comme ci-dessous:    

Je veux calculer 645,75/24

1. je pose ma division
2. on a partagé la partie entière du nombre,maintenant on va partager la partie décimale.
3. j'abaisse le 7 puis je mets la virgule après le 5 du quotient
4. je continue la division après la virgule ... et j obtiens :645,75/25 = 25,83                                                                   

                     Les nombres décimaux (1).

Un nombre décimal peut s' écrire sous forme d' une fraction décimale. 

Il comporte une partie entière  et une partie décimal séparées par une virgule.

On peut lire ce nombre ainsi:

9 virgule 562

9 unités et 562 millièmes

9 unités 5 dixièmes 6 centièmes 2 millièmes

Un tableau est parfois indispensable (voici le tableau minimum).

34 unités et 7 millièmes=34+7/1000=34,007

1 unité et 342 millièmes=1+342/1000=1,342

3 unités et 9 centièmes=3+9/100=3,09

4 unités et 5 millièmes=4+5/1000=4,005

7 unités et 25 centièmes=7+25/100=7,25